1. 复杂度、二分法、与异或运算

1.1 二分法

只要能构建出排他性的逻辑就可以用二分，比如说我虽然不知道左边可不可以，但我知道右边一定不可以，那么就可以二分。

1.2 异或运算

1.2.1 异或运算就是无进位的加法运算。

1.2.2 异或运算的应用

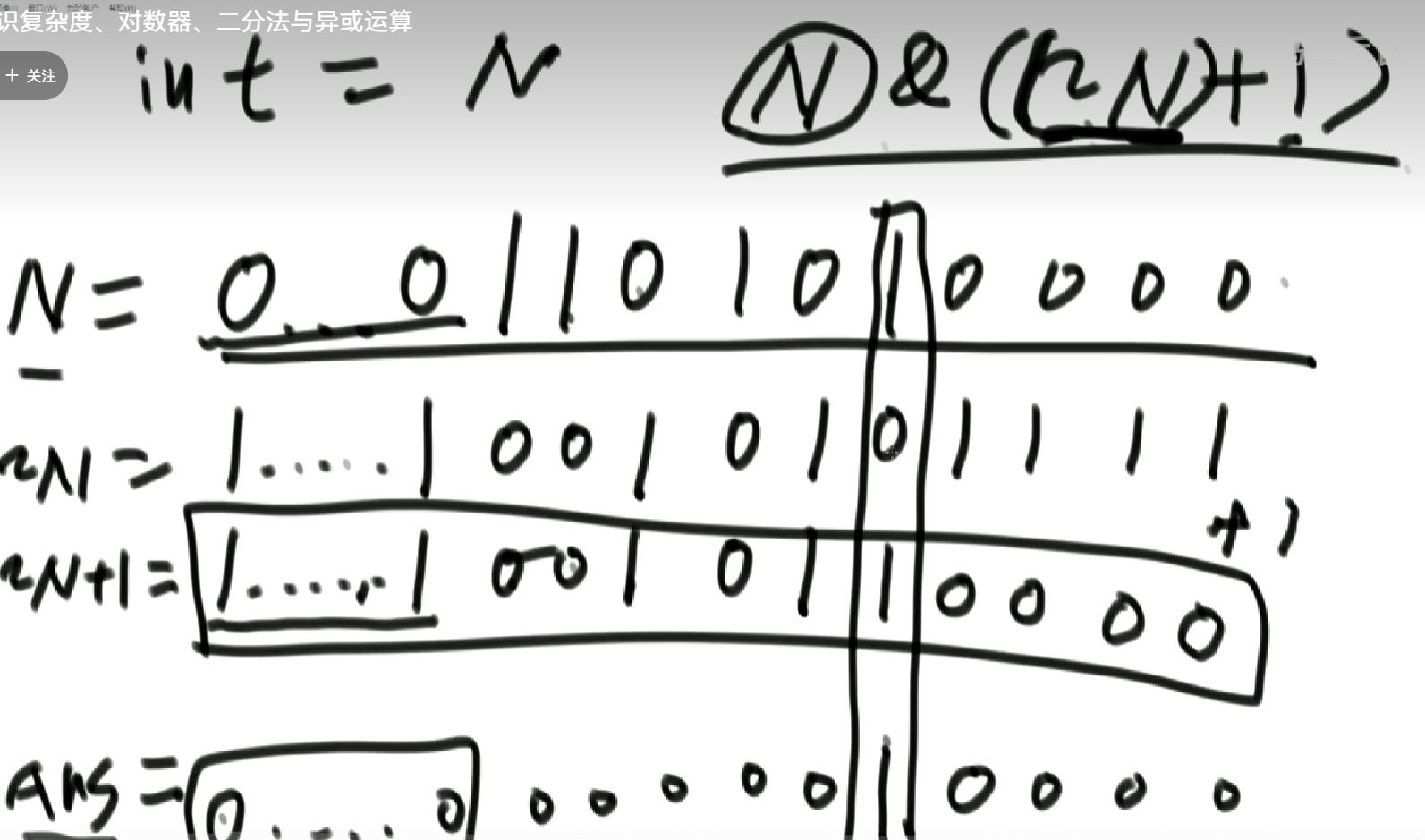
怎么把一个数字（int）最右侧的1提取出来？（注意是最右侧的1）

答案为：N&((~N)+1)，N取反首先会让最右侧1（记为1r）的右边的0变为1，让1r左边的1变0，0变1，然后加一会使1r右边的1依次进位变成0，直到进位到1r为止，此时1r变为1，最后与运算，因为1r左边取反了所以全为0，1r右边进位了全为0，得到结果

2. 二叉树

2.1 先序、中序、后序遍历（非递归实现）

先序

（1）弹打印

（2）如有右，压入右

（3）如有左，压入左

后序

上面先序是中左右，那么改变压栈顺序为中右左，倒过来就是左右中。

（1）弹加入另外一个栈

（2）如有左，压入左

（3）如有右，压入右

（4）从另外那个栈弹出一个打印一个

中序

（1）整条左边界依次入栈

（2）条件（1）不成立时，弹出打印，来到弹出结点的右树上继续条件（1）

2.2 二叉树递归套路

（1）假设以x为头，假设可以问x左树和x右树要任何信息。

（2）在上一步的假设下，讨论以x为头节点的树，得到答案的可能性（最重要的一步，常见分类：这道题的答案跟x有关和跟x无关）。

（3）列出所有可能性后，确定到底需要向左树和右树要什么样的信息。

（4）把左树信息和右树信息求全集，就是一棵子树都需要返回的信息S。

（5）递归函数都返回S，每一棵子树都这么要求。

（6）写代码，在代码中考虑如何把左树的信息和右树的信息整合出整棵树的信息。

2.3 堆和排序是解决贪心问题的常用技巧

2.4 二叉树的序列化（只能前序和后序）

要想实现反序列方法，首先要构造 root 节点。前序遍历得到的 nodes 列表中，第一个元素是 root 节点的值；后序遍历得到的 nodes 列表中，最后一个元素是 root 节点的值。

但对于中序遍历来说，root 的值被夹在两棵子树的中间，也就是在 nodes 列表的中间，我们不知道确切的索引位置，所以无法找到 root 节点，也就无法进行反序列化。

2.5 搜索二叉树（BST）的定义

如果该二叉树的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；它的左右子树也为二叉搜索树。

3. 图

4. 暴力递归

暴力递归就是尝试

把问题转化为规模缩小了的同类问题的子问题
有明确的不需要继续进行递归的条件
有当得到了子问题结果之后的决策过程
不记录每一子问题的解

5. 动态规划

5.1 四种尝试模型

（1）从左往右尝试

（2）范围上尝试

（3）多样本位置全对应尝试（一个做行、一个做列，而且往往是根据结尾位置怎么样来划分可能性）

（4）寻找业务限制尝试

（5）外部信息变成有效几个参数往下推

5.2 设计暴力递归过程的原则

（1）每一个可变参数类型，一定不要比int类型更加复杂

（2）原则（1）可以违反，让类型突破到一维线性结构，那必须是唯一可变参数

（3）如果发现原则（1）被违反，但不违反原则（2），只需要做到记忆化搜索即可

（4）可变参数的个数，能少则少

6. 单调队列

求窗口最大值
双端队列中的数据一定是严格从大到小的，双端队列维持的是在依次过期的情况下成为最大值的可能性，当有一个值cur需要从队尾加入队列时，如果比此时队尾的值大，将队尾值弹出，因为cur比队尾值大而且比队尾值晚过期，所以此时的队尾值不会再成为最大值了，直接弹出即可，重复此过程直到队列为空或队列末尾的值大于cur，将cur加入队尾。

7. 单调栈

找到左右两边离一个数最近的比他小（大）的那个数，下面的图是证明

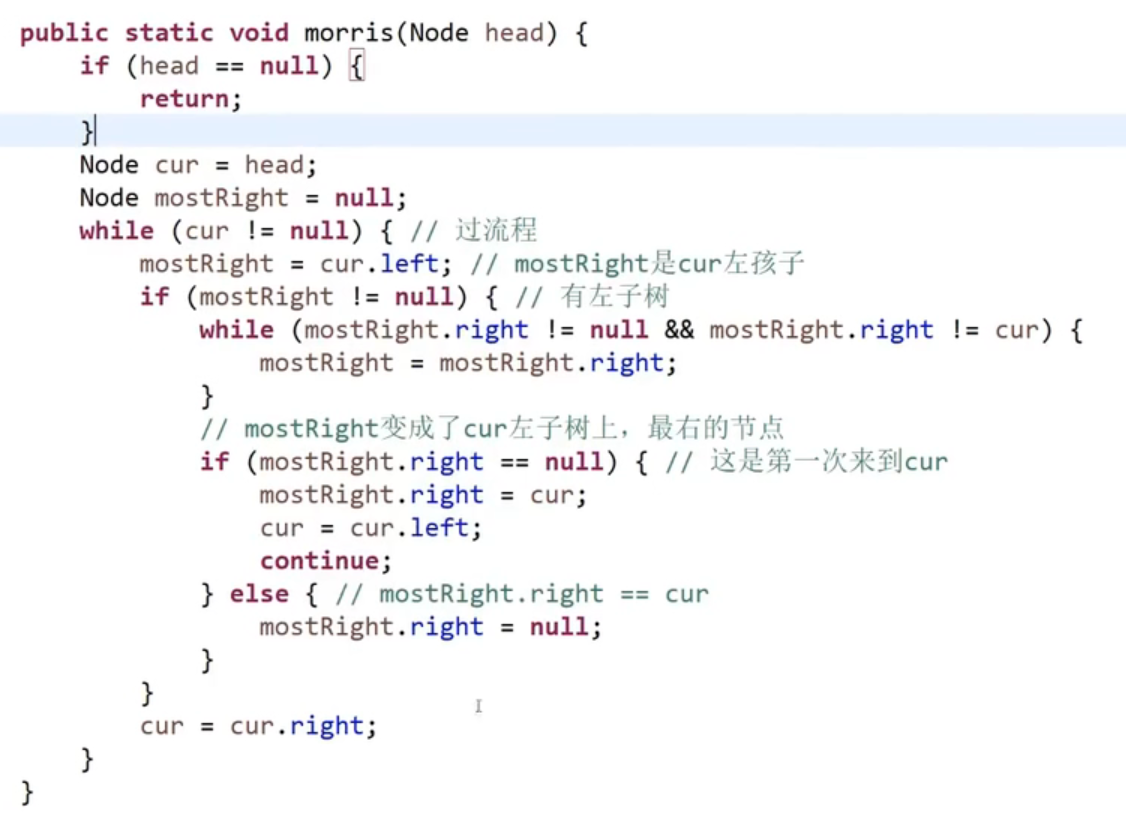
8. Morris遍历

遍历的规律：有左子树的结点会经过两次，没有左子树的结点只会经过一次，下面是Morris遍历的代码

9. 有序表

9.1 有序表的时间复杂度

有序表的所有操作（增删改查）时间复杂度都是O(logN)。

9.2 实现有序表的数据结构

红黑树、AVL树、SizeBalanceTree（简称SB树）、SkipList（跳表）

9.3 导致平衡性失效的四种情况

（1）LL型：我的左孩子的左子树过长导致平衡性失效。头节点单次右旋就可以调整

（2）RR型：我的右孩子的右子树过长导致平衡性失效。头节点单次左旋就可以调整

（3）LR型：我的左孩子的右子树（左孩子的右子树的头节点记为X）过长导致平衡性失效。调整方法是让X节点作为头部

（4）RL型：我的右孩子的左子树（右孩子的左子树的头节点记为X）过长导致平衡性失效。调整方法是让X节点作为头部

10. 刷题技巧

10.1 预处理技巧（预处理结构）

生成前缀累加和数组作为预处理结构。
某一个子数组可以累加生成的范围是1-range，对下一个数cur分情况讨论

（1）cur>range+1,为了充分利用前面这个范围，需要补充range+1这个数，让范围扩大到

1-（2*range+1）。

（2）cur<=range+1，那么可以直接累加使范围变为1-range+cur。

10.2 根据数据量猜解法

根据输入参数范围看菜下饭，代码常数级别的操作在10的8次方以内。下面举一个例子，说明怎么根据数据范围选择不同的方法。

花最少钱通过所有怪兽

int[] d，d[i]：i号怪兽的能力

int[] p，p[i]：i号怪兽要求的钱

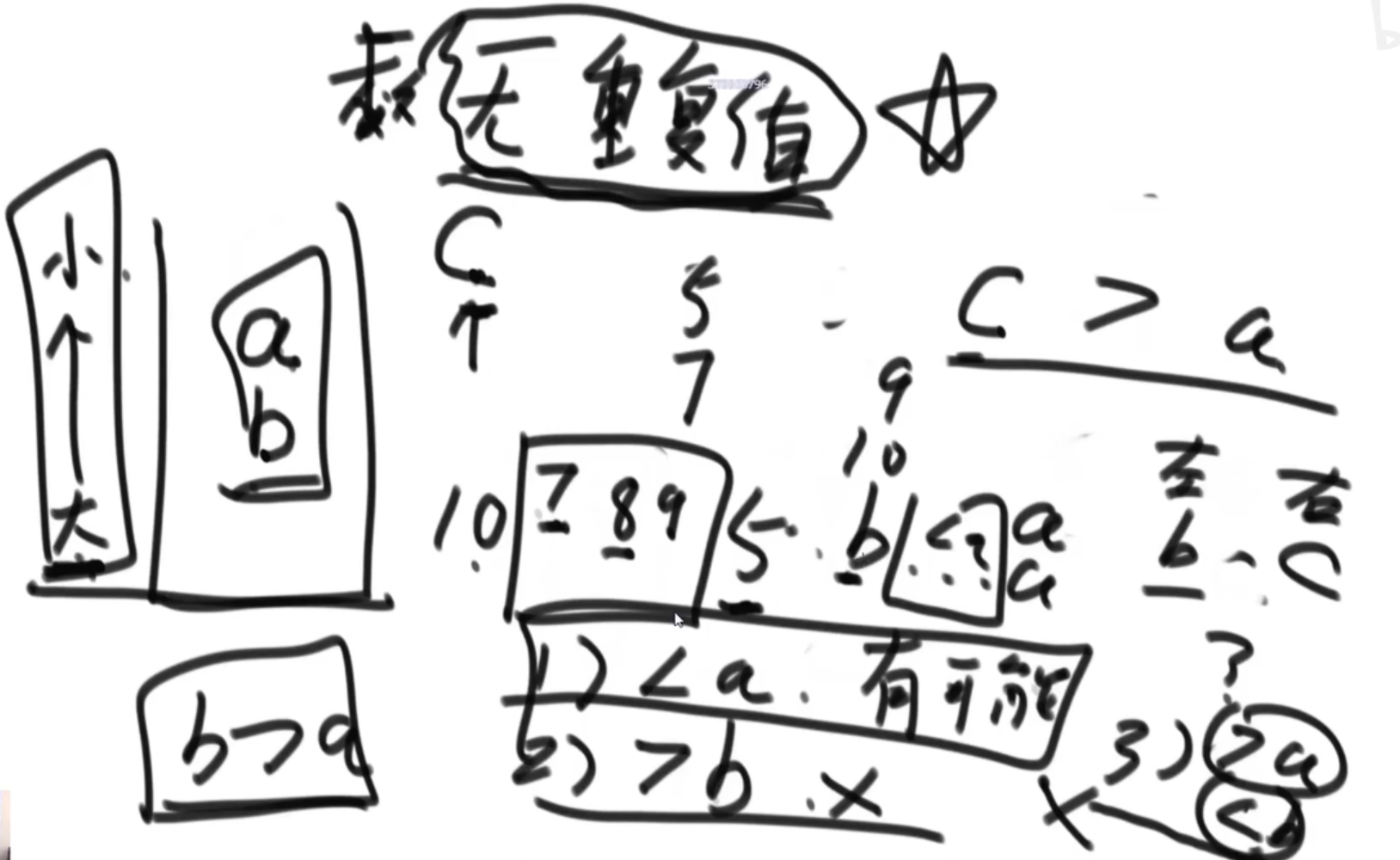
开始时你的能力是0，你的目标是从0号怪兽开始，通过所有的怪兽。

如果你当前的能力，小于i号怪兽的能力，你必须付出p[i]的钱，贿赂这个怪兽，然后怪兽就会加入你，他的能力直接累加到你的能力上；如果你当前的能力，大于等于i号怪兽的能力，你可以选择直接通过，你的能力并不会下降，你也可以选择贿赂这个怪兽，然后怪兽就会加入你，他的能力直接累加到你的能力上。

返回通过所有的怪兽，需要花的最小钱数。

分析

如果你的能力大于等于怪兽的能力，有两种选择：

第一种：直接通过，也不花钱，能力也不增长
第二种：贿赂怪兽，花钱，能力提升

如果你的能力小于怪兽的能力，只能花钱贿赂怪兽，然后能力值提升

方法一：暴力递归，ability：当前你所具有的能力，index：当前来到第index个怪兽的面前，目前你的能力是ability，你来到了index号怪兽的面前，如果要通过后续所有的怪兽，请返回需要花的最少钱数。

方法二：动态规划，由暴力递归发现只有两个可变参数（ability，index），准备一张二维dp表，index号怪兽做行，ability能力做列，index的变化范围0~N，ability的变化范围0~sum，所有能力加起来为sum。

方法三：动态规划，如果能力范围变化很大，可能导致dp表过大，导致方法执行效率不高，重新定义dp，dp[i][j]含义：能经过0~i的怪兽，且花钱为j（花的钱严格等于j）时的武力值最大是多少？

分析可能性：

可能性一：为当前怪兽花钱
可能性二：不为当前怪兽花钱

总结：如果sum能力值变化范围不大，则方法二就可以，如果sum变化范围很大，则方法三是最优解，这道题属于根据数据量猜解法。

实现

暴力递归

public static long func1(int[] d, int[] p) {
    return process(d, p, 0, 0);
}

// 当前你的能力是ability，来到index号怪兽面前，后续通过所有关需要花的最少的钱
public static long process(int[] d, int[] p, int ability, int index) {
    if (index == d.length) { // base case
        return 0;
    }
    // 当前的能力小于当前怪兽的能力，没得选，只能花钱贿赂，花了钱能力就增长
    if (ability < d[index]) { 
        return p[index] + process(d, p, ability + d[index], index + 1);
    } else { // 可以贿赂，也可以不贿赂，两者取最小值
        return Math.min(
            p[index] + process(d, p, ability + d[index], index + 1),
            process(d, p, ability, index + 1)
        );
    }
}

第一种动态规划

public static long func2(int[] d, int[] p) {
    int sum = 0;
    for (int num : d) { // 累加所有能力值
        sum += num;
    }
    // 怪兽范围为0~N+1，能力范围为0~sum+1
    //dp[i][j]表示具有i能力的情况下通过[i...d.length-1]这些怪兽需要最少的钱
    long[][] dp = new long[d.length + 1][sum + 1];
    for (int index = d.length - 1; index >= 0; index--) { // 从下往上推
        for (int ability = 0; ability <= sum; ability++) {
            //如果这种情况发生，那么这个hp是递归过程中不会出现的状态
            //因为动态规划是对递归过程的优化，尝试过程碰不到的状态，直接跳过即可，不必计算
            if (ability + d[index] > sum) {
                continue;
            }
            // 当前具备的能力小于当前怪兽的能力，没得选，只能花钱贿赂怪兽，然后能力增长
            if (ability < d[index]) { 
                dp[index][ability] = p[index] + dp[index + 1][ability + d[index]];
            } else { // 当前具备的能力大于等于当前怪兽的能力：两种选择
                dp[index][ability] = Math.min(p[index] + dp[index + 1][ability + d[index]], dp[index + 1][ability]);
            }
        }
    }
    return dp[0][0];
}

第二种动态规划

public static long func3(int[] d, int[] p) {
    int sum = 0;
    for (int num : p) {
        sum += num;
    }
    // dp[i][j]含义：
    // 能经过0～i的怪兽，且花钱为j（花钱的严格等于j）时的武力值最大是多少？
    // 如果dp[i][j]==-1，表示经过0～i的怪兽，花钱为j是无法通过的，或者之前的钱怎么组合也得不到正好为j的钱数
    int[][] dp = new int[d.length][sum + 1];
    for (int i = 0; i < dp.length; i++) {
        for (int j = 0; j <= sum; j++) {
            dp[i][j] = -1;
        }
    }
    // 经过0～i的怪兽，花钱数一定为p[0]，达到武力值d[0]的地步。其他第0行的状态一律是无效的
    dp[0][p[0]] = d[0];
    for (int i = 1; i < d.length; i++) {
        for (int j = 0; j <= sum; j++) {
            // 可能性一，为当前怪兽花钱
            // 存在条件：
            // j - p[i]要不越界，并且在钱数为j - p[i]时，要能通过0～i-1的怪兽，并且钱数组合是有效的。
            if (j >= p[i] && dp[i - 1][j - p[i]] != -1) {
                dp[i][j] = dp[i - 1][j - p[i]] + d[i];
            }
            // 可能性二，不为当前怪兽花钱
            // 存在条件：
            // 0~i-1怪兽在花钱为j的情况下，能保证通过当前i位置的怪兽
            if (dp[i - 1][j] >= d[i]) {
                // 两种可能性中，选武力值最大的
                dp[i][j] = Math.max(dp[i][j], dp[i - 1][j]);
            }
        }
    }
    int ans = 0;
    // dp表最后一行上，dp[N-1][j]代表：
    // 能经过0～N-1的怪兽，且花钱为j（花钱的严格等于j）时的武力值最大是多少？
    // 那么最后一行上，最左侧的不为-1的列数(j)，就是答案
    for (int j = 0; j <= sum; j++) {
        if (dp[d.length - 1][j] != -1) {
            ans = j;
            break;
        }
    }
    return ans;
}

10.3 用递归函数解决字符串嵌套问题

定义函数f(String str, int i)，代表从str的i位置出发一直往后延申，直到遇到字符串的终止位置或者遇到’}’（大括号可根据题目要求定义）停，返回从i出发到停这段的处理结果和停的位置。上级函数遇到’{‘就去递归调用该函数进行求解得到结果，再接着往下进行处理。

10.4 找到无序数组中未出现的最小正整数

上图的算法可以做到时间复杂度O(N)，空间复杂度O(1)。

10.5 数组中的连续递增子数组

长度为n的数组中最多有n/2个连续上坡，如下图所示。

10.6 四边形不等式优化动态规划

题目需要满足三个特征，在填dp表是可以根据所填格子的上班一个格子和右边一个格子确定枚举的上下限

（1）数据情况特殊（比如都是正数，题目中的两个指标（问题）存在单调性）。

（2）是区间划分问题（给你一个范围让你用给定的东西（给定多少个数）去搞定）。

（3）有枚举行为。

（4）每一个格子不同时依赖本行和本列。如果一个格子只依赖自己本行的值，列从左到右枚举，每一行从下到上，每个格子左边和下边给你提供下界和上界；如果一个格子只依赖本行的值，行从上往下枚举，每一列从右往左算，每个格子的上边和右边给你提供下界和上界。

10.7 二分答案法

根据题目问题分析出答案所在的范围（粗略一点也无所谓），然后在答案范围上二分去验证。

10.8 子串、子数组相关的问题解法

首先想以0位置结尾（或开头）该问题答案是什么，以1位置结尾（或开头）答案是什么，以2位置结尾（或开头）答案是什么。。。

10.9 最长递增子序列（子序列可以不连续）

算法原型：动态规划+贪心+二分查找

考虑一个简单的贪心，如果我们要使上升子序列尽可能的长，则我们需要让序列上升得尽可能慢，因此我们希望每次在上升子序列最后加上的那个数尽可能的小。

基于上面的贪心思路，我们维护一个数组 d[i] ，表示长度为 i 的最长上升子序列的末尾元素的最小值，用 len 记录目前最长上升子序列的长度，起始时 len 为 1，d[1]=nums[0]。

同时我们可以注意到 d[i] 是关于 i 单调递增的。因为如果 d[j]≥d[i] 且 j<i，我们考虑从长度为 i 的最长上升子序列的末尾删除 i-j个元素，那么这个序列长度变为 j ，且第 j 个元素 x（末尾元素）必然小于 d[i]（因为从第j个元素到第i个元素是单调递增的），也就小于 d[j]。那么我们就找到了一个长度为 j 的最长上升子序列，并且末尾元素比 d[j] 小，从而产生了矛盾。因此数组 d 的单调性得证。

我们依次遍历数组 nums 中的每个元素，并更新数组 d 和 len 的值。

如果 nums[i]>d[len] 则更新len=len+1，否则在 d[1…len]中找满足 d[i−1]<nums[j]<d[i] 的下标 i，并更新 d[i]=nums[j]。

根据 d 数组的单调性，我们可以使用二分查找寻找下标 i，优化时间复杂度。

最后整个算法流程为：

设当前已求出的最长上升子序列的长度为 len（初始时为 1），从前往后遍历数组 nums，在遍历到 nums[i] 时：

如果 nums[i]>d[len] ，则直接加入到 d 数组末尾，并更新 len=len+1；
否则，在 d 数组中二分查找，找到最后一个比 nums[i] 小的数 d[k]，并更新 d[k+1]=nums[i]。（也就是长度为k的递增子序列末尾元素的最小值为d[k]，因为这是最后一个比nums[i]小的数，所以d[k+1]一定大于nums[i]，所以长度为k+1的递增子序列末尾元素的最小值可以更新）。

class Solution {
    public int lengthOfLIS(int[] nums) {
        int len = 1, n = nums.length;
        if (n == 0) {
            return 0;
        }
        int[] d = new int[n + 1];
        d[len] = nums[0];
        for (int i = 1; i < n; ++i) {
            if (nums[i] > d[len]) {
                d[++len] = nums[i];
            } else {
                // 如果找不到说明所有的数都比 nums[i] 大，
                //此时要更新 d[1]，所以这里将 pos 设为 0
                int l = 1, r = len, pos = 0; 
                while (l <= r) {
                    int mid = (l + r) >> 1;
                    if (d[mid] < nums[i]) {
                        pos = mid;
                        l = mid + 1;
                    } else {
                        r = mid - 1;
                    }
                }
                d[pos + 1] = nums[i];
            }
        }
        return len;
    }
}

10.10 假设答案法

先假设出该题的答案，然后分析答案的一些性质，设计一个复杂度尽量低的流程把答案找出来。

10.11 压缩数组技巧

将矩阵每一行加起来成为一个数组，看到子矩阵的问题可以先想子数组是怎么处理的。

10.12 通过平凡解剪枝

如果某一个递归跑不完，那么可以通过找一个平凡解，当递归得到的解比平凡解还差的时候就提前退出了。

11. 线段树（区间修改树）

更快速的、区间的更改、查询一些东西。实现一种数据结构使得以下三种计算的时间复杂度为O(logN)
void add(arr, L, R, V); ：将arr数组中的第L到R的数都增加V
void update(arr, L, R, V);：将arr数组中的第L到R的数都修改为V
int getSum(arr, L, R);：将arr数组中的第L到R的数相加返回累加和

需要多少空间：假设数据量为N，N如果不是2的某次方也补齐为2的某次方，最多需要4*N的空间，线段树的左右节点都是根据父节点依次二分得出的。

public class SegmentTree {
    private int MAXN;
    private int[] arr;
    private int[] sum;
    private int[] lazy;
    private int[] change;
    private boolean[] update;

    public SegmentTree(int[] origin) {
        MAXN = origin.length + 1;
        arr = new int[MAXN];
        for (int i = 0; i < MAXN; i++) {
            arr[i] = origin[i - 1];
        }
        sum = new int[MAXN << 2];
        lazy = new int[MAXN << 2];
        change = new int[MAXN << 2];
        update = new boolean[MAXN << 2];
    }

    private void pushUp(int rt) {
        sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
    }

    /**
     * 将任务下发
     * 
     * @param rt 当前的目标节点
     * @param ln 目标节点左子树的节点个数
     * @param rn 目标节点柚子树节点个数
     */
    private void pushDown(int rt, int ln, int rn) {
        if (update[rt]) {
            update[rt << 1] = true;
            update[rt << 1 | 1] = true;
            change[rt << 1] = change[rt];
            change[rt << 1 | 1] = change[rt];
            lazy[rt << 1] = 0;
            lazy[rt << 1 | 1] = 0;
            sum[rt << 1] = change[rt] * ln;
            sum[rt << 1 | 1] = change[rt] * rn;
            update[rt] = false;
        }
        // 下发上次更新后执行的add操作
        if (lazy[rt] != 0) {
            lazy[rt << 1] += lazy[rt];
            lazy[rt << 1 | 1] += lazy[rt];
            sum[rt << 1] += lazy[rt] * ln;
            sum[rt << 1 | 1] += lazy[rt] * rn;
            lazy[rt] = 0;
        }
    }

    public void build(int l, int r, int rt) {
        if (l == r) {
            sum[rt] = arr[l];
            return;
        }
        int mid = (l + r) >> 1;
        build(l, mid, rt << 1);
        build(mid + 1, r, rt << 1 | 1);
        pushUp(rt);
    }

    public void update(int L, int R, int C, int l, int r, int rt) {
        // 全包了,只懒更新根节点
        if (L <= l && r <= R) {
            update[rt] = true;
            change[rt] = C;
            sum[rt] = C * (r - l + 1);
            lazy[rt] = 0;
            return;
        }
        // 需要下发
        int mid = (l + r) >> 1;
        pushDown(rt, mid - l + 1, r - mid);
        if (L <= mid) {
            update(L, R, C, l, mid, rt << 1);
        }
        if (R > mid) {
            update(L, R, C, mid + 1, r, rt << 1 | 1);
        }
    }

    /**
     * 懒添加
     * 
     * @param L  任务左
     * @param R  任务右
     * @param C  加的数值
     * @param l  收到任务的数组左
     * @param r  收到任务的数组右
     * @param rt 根节点
     */
    public void add(int L, int R, int C, int l, int r, int rt) {
        if (L <= l && r <= R) {
            // 任务将当前的数组全包了,不用下传了
            sum[rt] += C * (r - l + 1);
            lazy[rt] += C;
            return;
        }
        // 下发任务
        int mid = (l + r) >> 1;
        // 下发之前的lazy add任务
        pushDown(rt, mid - l + 1, r - mid);
        if (L <= mid) {
            add(L, R, C, l, mid, rt << 1);
        }
        if (R > mid) {
            add(L, R, C, mid + 1, r, rt << 1 | 1);
        }
        pushUp(rt);
    }

    public long query(int L, int R, int l, int r, int rt) {
        if (L <= l && r <= R) {
            return sum[rt];
        }
        int mid = (l + r) >> 1;
        pushDown(rt, mid - l + 1, r - mid);
        long ans = 0;
        if (L <= mid) {
            ans += query(L, R, l, mid, rt << 1);
        }
        if (R > mid) {
            ans += query(L, R, mid + 1, r, rt << 1 | 1);
        }
        return ans;
    }
}

12. 设计数据结构的题目（一般是根据老结构改）

12.1 带有setAll功能的哈希表

要求：使setAll、get、put方法的时间复杂度仍然是O(1)

解答：加入三个变量，long类型的time变量记录时间戳，一开始初始化为0，每次调用setAll方法，put方法都让时间戳加一，哈希表的value封装为数据和时间戳的值；long类型的setAllTime记录最近一次调用setAll方法的时间戳，每次调用setAll方法就更新；int类型的all变量记录当前的all，调用setAll就更新。调用get方法时先将得到的value的时间戳和setAllTime比较一下来决定返回值。

13. 字符串问题

13.1 返回字符串中有多少个字面值不同的子序列

public static int solve(char[] str) {
    if (str == null || str.length == 0) {
        return 0;
    }

    // 以每个字符结尾的集合数目
    int[] dp = new int[26];

    // 集合数目，初始空集
    int all = 1;

    for (char c : str) {
        // 集合数目扩大一倍，减去重复
        int add = all - dp[c - 'a'];
        all += add;
        dp[c - 'a'] += add;
    }

    // 结果不含空集
    return all - 1;
}

14. 一些小结论

14.1 合并相邻数字

n个数每次只能相邻k个数合并，最终能不能合成一个数：如果(n-1)%(k-1)==0，就能合并成一个数，如果大于0就不能合并。

14.2 有单调性的问题就要想到滑动窗口

14.3 答案流程的优化

从两方面入手，自己的数据状况，所要求解的标准。

15. index tree

15.1 使用场景

在对一个数据集进行一些例如区间 [L,R] 求和的问题的时候（可以更改数据集中某一个元素的值，并且能查询任意范围上的累加和），想通过一个比较快的数据结构来完成，可以使用indexTree，它可以达到 O(logN) 的时间复杂度。

15.2 算法思想

构建一个help数组，如下图

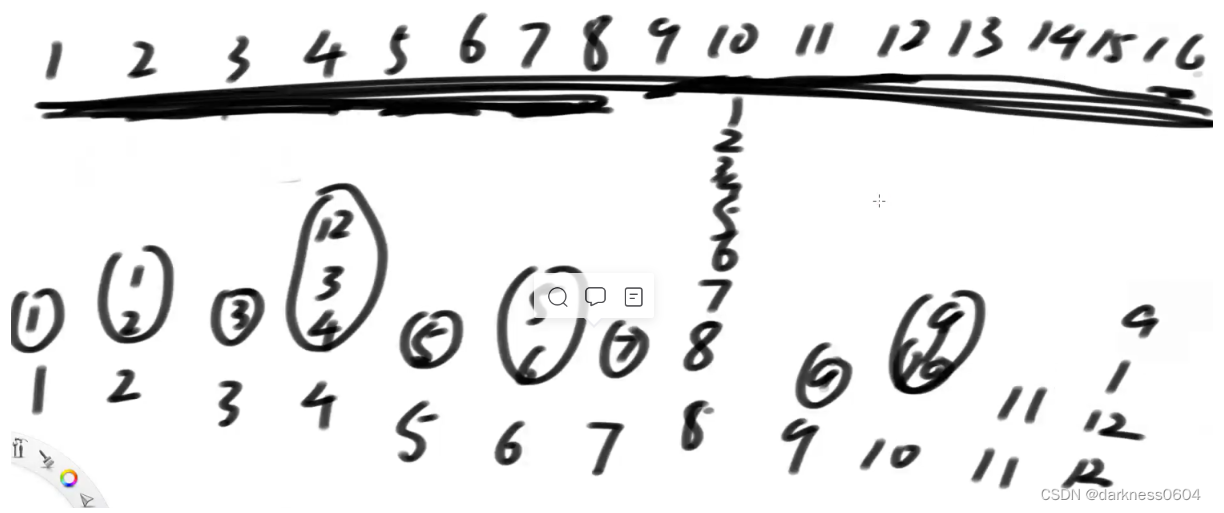
作为一个help数组，有如下特点：

help数组的有效位置从1位置开始
采用“配对”的方式在位置上存放值，因此以图上为例，我们来描述一个这个过程：

1：1位置上只有自己，因此只存放1位置的值
2：之前有一个1位置，所以与2位置配对，组成一对，所以此位置存放1,2位置的值
3: 3位置往前看，忽视已经配对的位置，因此只有它自己，因此只存放3位置的值
4：之前有一个3位置，所以可以配对3,4；但3,4配对之后又可以和之前配对的1,2进行组配对，因此此处位置就存放1,2,3,4的值
5：5位置往前看，忽视已经配对的位置，因此只有它自己，因此只存放5位置的值
6：之前有一个5位置，所以可以配对5,6，组成一对，所以此位置存放5,6位置的值
7：7位置往前看，忽视已经配对的位置，因此只有它自己，因此只存放7位置的值
8：8位置之前有一个7位置，所以可以配对7,8,，但因此和之前的5,6又可以配在一起形成5,6,7,8，此时又可以和之前形成的1,2,3,4配对，形成1,2,3,4,5,6,7,8，因此8位置存放1-8

此后的变换过程不再赘述，以这种规律进行数值的存放。

求help数组任意位置的所管辖的数值和

如果给定help数组的一个二进制形式的位置索引，想要得到这个位置存放了哪些值的累加和怎么办？
其中存在这样一个规律，把该位置的二进制形式最右侧的1去掉，再+1得到的数，就是这个累加和范围的起始索引，结束索引就是它位置自身，我们不妨进行举例说明：

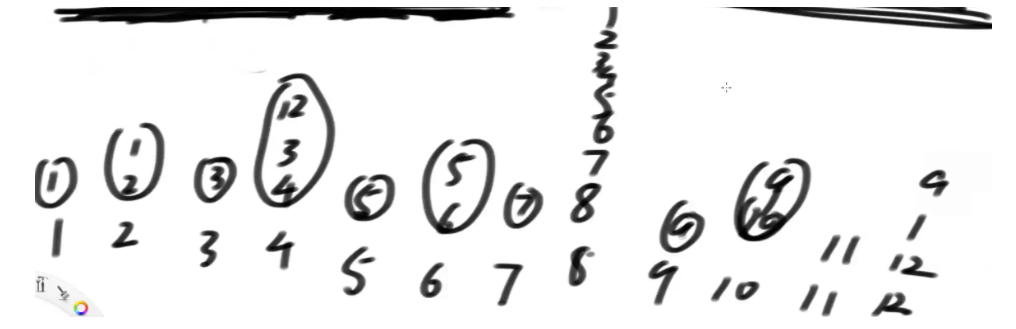
针对图上的位置：
1、假如我想知道位置4上管辖了哪些数的累加和怎么求？
4的二进制形式是：0100，我们去掉最右侧的1，变成：0000，再+1，得到0001，这个的十进制就是1，因此我们可以确定累加和的范围起始索引是1，即，4位置存放的是1~4的累加和

2、假如我想知道位置5上管辖了哪些数的累加和怎么求？
5的二进制形式是：0101，我们去掉最右侧的1，变成：0100，再+1，得到0101，这个的十进制就是5，因此我们可以确定累加和的范围起始索引是5，即，5位置存放的是5~5的累加和

利用help数组的机制，求1-N的累加和

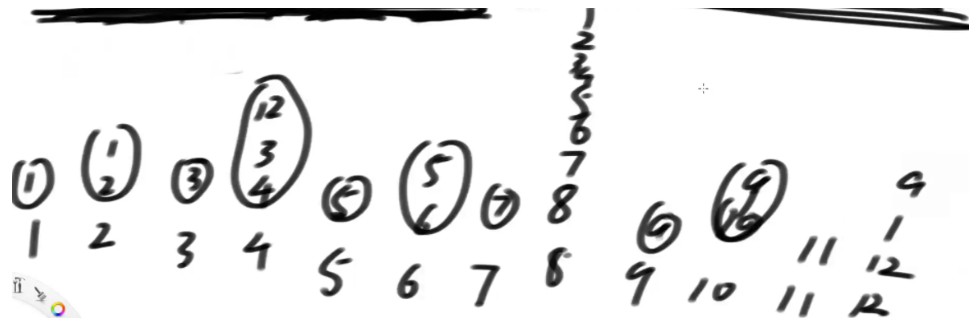
我们通过上面，已经知道help数组的机制，那如何通过它来实现1-N的累加和问题呢？还是通过上图来举例：
如果我要求1~7位置的累加和，怎么求？

准备一个累加值

7的位置索引二进制表示为0111，通过上面获得指定位置所管辖的范围值的累加和，可以得到的7位置管辖的就是7~7的累加值，把此位置的值加入累加值

接着，对7的二进制移除最右侧的1，得到0110，也就是位置6（存放5,6的累加值），把此位置的值加入累加值，

接着，对位置6的位置的二进制移除最右侧的1，得到0100，也就是位置4（存放1-4的累加值），把此位置的值加入累加值，

接着，对位置4的二进制移除最右侧的1，得到0000，此时发现得到的值已经是0，不进行任何操作，并终止操作

15.3 代码实现

// 下标从1开始！
public  class IndexTree {

    private int[] tree;
    private int N;

    // 0位置弃而不用！
    public IndexTree(int size) {
        N = size;
        tree = new int[N + 1];
    }

    // 1~index 累加和是多少？
    public int sum(int index) {
        int ret = 0;
        while (index > 0) {
            ret += tree[index];
            index -= index & -index;
        }
        return ret;
    }

    // index & -index : 提取出index最右侧的1出来
    // index :           0011001000
    // index & -index :  0000001000
    public void add(int index, int d) {
        //当添加到当前位置时，哪些位置会收到影响？依次对它们也进行累加此值
        //可以自己举个例子推导一下 index+index最右侧的1 的结果就是下一个会被影响的位置
        while (index <= N) {
            tree[index] += d;
            index += index & -index;
        }
    }
}

16. 一些经典问题

16.1 Nim博弈问题

原题意：先手后手从数组中拿数字，每次只能从数组的一个位置拿，可以拿任意数量x（0<x<=数组当前值），谁最先让数组全为0就赢了。

解答：先手一直让数组的异或和为0，那么最后赢的状态也是异或和为0，如果初始状态异或和不为0，先手总可以拿一定数量使得异或和为0，所以先手赢；如果初始异或和为0，先手不管怎么拿都会让异或和不为0，后手可以一直让异或和为0，后手赢。

33.高级进阶班-5_哔哩哔哩_bilibili

16.2 求有向图的强连通分量

【图论】Tarjan算法详解-CSDN博客