Discrete Math

BFS（广度优先搜索）

我们采用示例图来说明这个过程，在搜索的过程中，初始所有节点是白色（代表了所有点都还没开始搜索），把起点V0标志成灰色（表示即将辐射V0），下一步搜索的时候，我们把所有的灰色节点访问一次，然后将其变成黑色（表示已经被辐射过了），进而再将他们所能到达的节点标志成灰色（因为那些节点是下一步搜索的目标点了），但是这里有个判断，就像刚刚的例子，当访问到V1节点的时候，它的下一个节点应该是V0和V4，但是V0已经在前面被染成黑色了，所以不会将它染灰色。这样持续下去，直到目标节点V6被染灰色，说明了下一步就到终点了，没必要再搜索（染色）其他节点了，此时可以结束搜索了，整个搜索就结束了。然后根据搜索过程，反过来把最短路径找出来，下图中把最终路径上的节点标志成绿色。

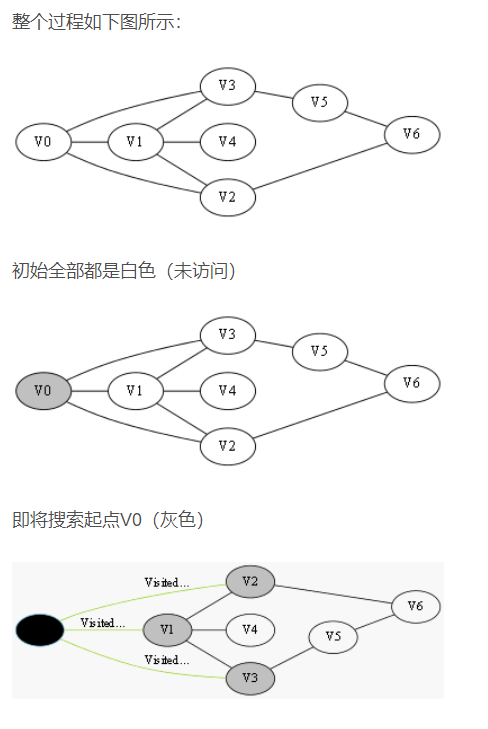
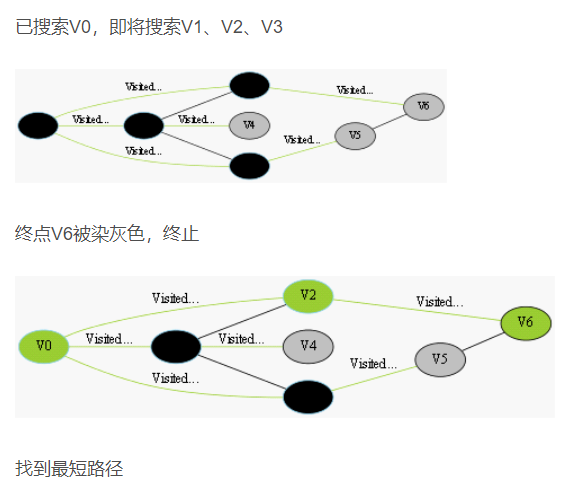
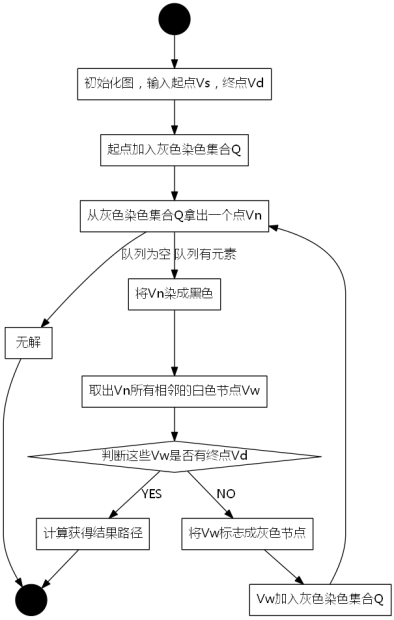
为了便于进行搜索，要设置一个表存储所有的结点。由于在广度优先搜索算法中，要满足先生成的结点先扩展的原则，所以存储结点的表一般采用队列这种数据结构。

在编写程序时，可用数组q模拟队列。front和rear分别表示队头指针和队尾指针，初始时front=rear=0。

元素x入队操作为 q[rear++]=x;

元素x出队操作为 x =q[front++];

广度优先搜索算法的搜索步骤一般是：

（1）从队列头取出一个结点，检查它按照扩展规则是否能够扩展，如果能则产生一个新结点。

（2）检查新生成的结点，看它是否已在队列中存在，如果新结点已经在队列中出现过，就放弃这个结点，然后回到第（1）步。否则，如果新结点未曾在队列中出现过，则将它加入到队列尾。

（3）检查新结点是否目标结点。如果新结点是目标结点，则搜索成功，程序结束；若新结点不是目标结点，则回到第（1）步，再从队列头取出结点进行扩展。

最终可能产生两种结果：找到目标结点，或扩展完所有结点而没有找到目标结点。

对于广度优先搜索算法来说，问题不同则状态结点的结构和结点扩展规则是不同的，但搜索的策略是相同的。广度优先搜索算法的框架一般如下：

void  BFS（）

{

    队列初始化；

    初始结点入队；

    while （队列非空）

    {  

          队头元素出队，赋给current；

          while  （current 还可以扩展）

          {

              由结点current扩展出新结点new；

              if  （new 重复于已有的结点状态） continue;

              new结点入队；

              if  (new结点是目标状态)

              {

                    置flag= true;    break; 

               }

          }

      }

}

DFS（深度优先搜索）

深度优先搜索（缩写DFS）有点类似广度优先搜索，也是对一个连通图进行遍历的算法。它的思想是从一个顶点V0开始，沿着一条路一直走到底，如果发现不能到达目标解，那就返回到上一个节点，然后从另一条路开始走到底，这种尽量往深处走的概念即是深度优先的概念。下面是dfs的框架代码

/**
 * DFS核心伪代码
 * 前置条件是visit数组全部设置成false
 * @param n 当前开始搜索的节点
 * @param d 当前到达的深度，也即是路径长度
 * @return 是否有解
 */
bool DFS(Node n, int d){
    if (d == 4){//路径长度为返回true，表示此次搜索有解
        return true;
    }

    for (Node nextNode in n){//遍历跟节点n相邻的节点nextNode，这里体现了回溯
        if (!visit[nextNode]){//未访问过的节点才能继续搜索

            //例如搜索到V1了，那么V1要设置成已访问
            visit[nextNode] = true;

            //接下来要从V1开始继续访问了，路径长度当然要加

            if (DFS(nextNode, d+1)){//如果搜索出有解
                //例如到了V6，找到解了，你必须一层一层递归的告诉上层已经找到解
                return true;
            }

            //重新设置成未访问，因为它有可能出现在下一次搜索的别的路径中
            visit[nextNode] = false;

        }
        //到这里，发现本次搜索还没找到解，那就要从当前节点的下一个节点开始搜索。
    }
    return false;//本次搜索无解
}

再贴一段DFS的伪码

int check(参数)
{
    if(满足条件)
        return 1;
    return 0;
}
 
void dfs(int step)
{
        判断边界
        {
            相应操作
        }
        尝试每一种可能，会用到for循环
        {
               满足check条件
               标记
               继续下一步dfs(step+1)
               恢复初始状态（回溯的时候要用到）
        }
} 

深度与广度的比较

我们假设一个节点衍生出来的相邻节点平均的个数是N个，那么当起点开始搜索的时候，队列有一个节点，当起点拿出来后，把它相邻的节点放进去，那么队列就有N个节点，当下一层的搜索中再加入元素到队列的时候，节点数达到了N^2，你可以想想，一旦N是一个比较大的数的时候，这个树的层次又比较深，那这个队列就得需要很大的内存空间了。

于是广度优先搜索的缺点出来了：在树的层次较深并且子节点数较多的情况下，消耗内存十分严重。广度优先搜索适用于节点的子节点数量不多，并且树的层次不会太深的情况。

那么深度优先就可以克服这个缺点，因为每次搜的过程，每一层只需维护一个节点。但回过头想想，广度优先能够找到最短路径，那深度优先能否找到呢？深度优先的方法是一条路走到黑，那显然无法知道这条路是不是最短的，所以你还得继续走别的路去判断是否是最短路？

于是深度优先搜索的缺点也出来了：难以寻找最优解，仅仅只能寻找有解。其优点就是内存消耗小，克服了刚刚说的广度优先搜索的缺点。