1. Shell

1. MyBatis

1.1 搭建MyBatis环境

2. Spring

2.1 IOC-控制反转，依赖注入

2.2 AOP-面向切面编程

2.3 声明式事务

Spring事务属性之7种传播行为-CSDN博客

3.SpringMVC

3.1 请求和响应

请求头和响应头的报文中的键是不区分大小写的，但是值区分大小写。

3.2 转发和重定向

业务处理成功一般使用重定向，失败则使用转发。

4. 一些额外的知识

4.1 DTD文件

文档类型定义（DTD）可定义合法的XML文档构建模块。它使用一系列合法的元素来定义文档的结构。

4.2 注解

java注解-最通俗易懂的讲解 - 知乎 (zhihu.com)

4.3 类加载器

CSDN博客-类加载器

4.4 post和get请求方式

post有请求体，get没有请求体。

4.5 Tomcat相关

Tomcat处理HTTP请求原理&线程池

微信小程序开发教程

发表于 2022-10-17 更新于 2023-02-18 分类于微信小程序开发

1. 前端

1.1 WXSS

1.1.1 尺寸单位

rpx：可以根据屏幕宽度进行自适应。规定屏幕宽度为750rpx。

1.1.2 样式的使用

静态的样式统一写到class中。style接受动态样式，在运行时进行解析，尽量避免将静态样式写到style中，以免影响渲染速度。

1.1.3 页面布局

Flex 布局语法教程 | 菜鸟教程 (runoob.com)，在display属性中使用flex布局，display:flex;

1.1.4 button按钮的属性

button按钮会有一些默认的样式，要通过style内嵌css来设置样式。

阅读全文 »

算法与数据结构（左程云）

发表于 2022-09-19 更新于 2023-02-18 分类于 LeetCode

1. 复杂度、二分法、与异或运算

1.1 二分法

只要能构建出排他性的逻辑就可以用二分，比如说我虽然不知道左边可不可以，但我知道右边一定不可以，那么就可以二分。

1.2 异或运算

1.2.1 异或运算就是无进位的加法运算。

1.2.2 异或运算的应用

怎么把一个数字（int）最右侧的1提取出来？（注意是最右侧的1）

答案为：N&((~N)+1)，N取反首先会让最右侧1（记为1r）的右边的0变为1，让1r左边的1变0，0变1，然后加一会使1r右边的1依次进位变成0，直到进位到1r为止，此时1r变为1，最后与运算，因为1r左边取反了所以全为0，1r右边进位了全为0，得到结果

阅读全文 »

条款01: 视C++ 为一个语言联邦

条款02: 尽量以 const, enum, inline 替换 #define

阅读全文 »

1. 结构化程序设计部分

1.1 数据类型

int x=8; x的取值范围被称为值集

阅读全文 »

LeetCode刷题笔记2

发表于 2022-09-11 更新于 2023-02-18 分类于 LeetCode

226. 翻转二叉树

方法一：递归

其实就是交换一下左右节点，然后再递归的交换左节点，右节点我们可以总结出递归的两个条件如下：

终止条件：当前节点为 null 时返回
交换当前节点的左右节点，再递归的交换当前节点的左节点，递归的交换当前节点的右节点

TreeNode *invertTree(TreeNode *root) {
    if (root == nullptr) {
        return nullptr;
    }
    TreeNode *temp = root->left;
    root->left = root->right;
    root->right = temp;
    invertTree(root->left);
    invertTree(root->right);
    return root;
}

方法二：迭代

递归实现也就是深度优先遍历的方式，迭代使用广度优先遍历，我们需要先将根节点放入到队列中，然后不断的迭代队列中的元素。
对当前元素调换其左右子树的位置，然后：

判断其左子树是否为空，不为空就放入队列
判断其右子树是否为空，不为空就放入队列

这样其实也是实现了二叉树的层序遍历

阅读全文 »

数据结构与算法分析

发表于 2022-09-07 更新于 2023-02-18 分类于数据结构与算法

1. 第一课

面向对象：封装、继承、多态。模块与模块之间尽量解耦合

2. 递归

约瑟夫环问题（递归解法）

假设：

初始情况： 0, 1, 2 ……n-2, n-1 (共n个人)

第一个人(编号一定是(m-1)%n,设之为(k-1) ) 出列之后，

剩下的n-1个人组成了一个新的约瑟夫环（以编号为k==m%n的人开始）:

k k+1 k+2 … n-2, n-1, 0, 1, 2, …,k-3, k-2

现在我们把他们的编号做一下转换：

x -> x’ （x‘代表新编号，x代表原编号 k==m%n）

k –> 0
k+1 –> 1
k+2 –> 2
…
…

k-3 –> n-3

k-2 –> n-2

变换后就完完全全成为了(n-1)个人报数的子问题，假如我们知道这个子问题的解：例如x’是最终的胜利者，那么根据上面这个表把这个x’变回去不刚好就是n个人情况的解吗！
x’ ->ｘ？(这正是从n-1时的结果反过来推n个人时的编号！)
0 -> k

1 -> k+1

2 -> k+2

…

n-3 -> k-3

n-2 -> k-2

变回去的公式　x=(x’+k)%n

那么，如何知道(n-1)个人报数的问题的解？只要知道(n-2)个人的解就行了。(n-2)个人的解呢？只要知道(n-3)的情况就可以了 —- 这显然就是一个递归问题：

令f[i]表示i个人玩游戏报m退出最后胜利者的编号，最后的结果就是f[n]

递推公式

f[1]=0;

f[n]=(f[n-1]+k)%n = (f[n-1] +m%n) % n = (f[n-1] + m) % n ; (n>1)

当然，当n==1时，直接返回0即可

public static int lastRemaining(int n, int m) {
    if (n == 1) {
        return 0;
    }
    return (lastRemaining(n - 1, m) + m) % n;
}

3. 链表

4.栈、队列

4.1 数组循环左移

假设数组a[7]={1,2,3,4,5,6,7}，向左移3个元素，输出结果为：4 5 6 7 1 2 3

对前3个元素逆序，变为{3,2,1,4,5,6,7}

对后4个元素逆序，变为{ 3,2,1,7,6,5,4 }

对所有元素逆序，变为{ 4,5,6,7,1,2,3 }

#include<stdio.h>

//[ster...end)，左边包含右边不包含
void reverse(int *a, int ster, int end)

{

    int temp;

    int s = end - 1;        //起始位置下标不变，终止位置-1

    while (ster < s)

    {

        temp = a[ster];

        a[ster] = a[s];

        a[s] = temp;

        ster++;

        s--;

    }

}

void main()

{

    int i, k, a[7] = { 1,2,3,4,5,6,7 };

    printf("先输入左移个数：\n");

    scanf("%d", &k);

    reverse(a, 0, k);

    reverse(a, k, 7);

    reverse(a, 0, 7);

    for (int i = 0; i < 7; i++)

    {

        printf("%d ", a[i]);

    }

}

4.2 表达式树

《数据结构》：中缀表达式转后缀表达式后缀表达式的计算

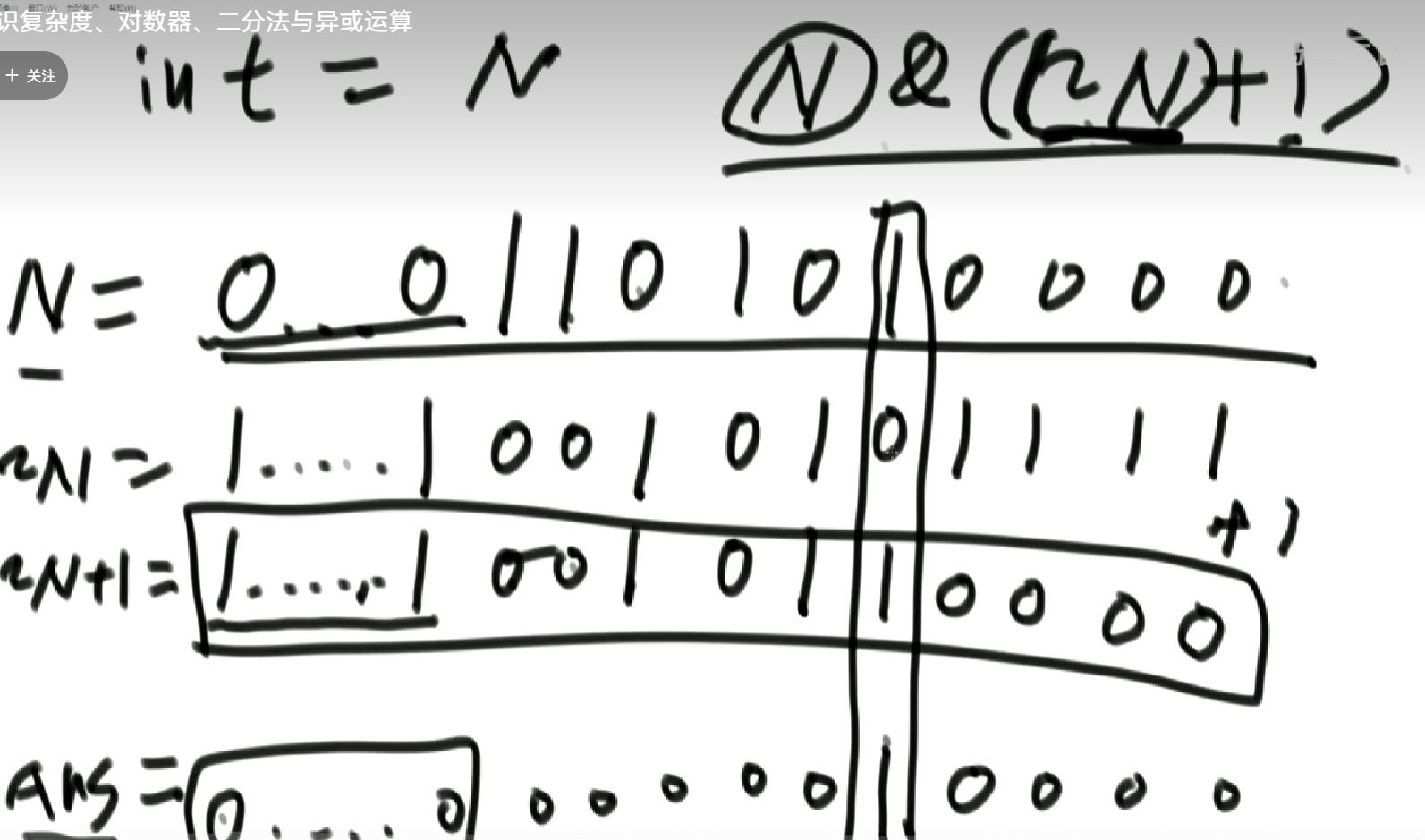
1. 整数除法

关于整数除法固有bug的一些解释。

固有bug就是结果的余数和除数相等或互为相反数。

对于这个不恢复余数的除法，我其实是有点困惑它的正确性如何成立的。经过一些思考，得出了一些或许可以增进一些理解的解释。首先我们考虑被除数和除数都是正数的情况，按照不恢复余数除法的上商规则，不难得出其实每一位商都会是正确的，因为上商判断时依据的也是新算出来的余数，也就是是否够减。但是最后的余数可能会有偏差，如果最后一步是不够减的，上商为0之后本来应该要在下一步实现恢复的，但是没有下一步了，因此我们要将余数加上一个被除数。两个负数相除的情形是类似的。但是需要注意的是一个负数除以它本身的情形，比如-8/（-8），算的时候我们得到-8 - 1*（-8）= 0，这时候如果看位串的符号位来说是变号了的，应该上商是0，然后余数现在也是0，但是在修正余数的时候由于0和-8符号位不同，要加上一个-8，余数变成-8，这显然是不合理的。对于这种情况需要加一个修正，即如果余数等于除数，那么余数减去除数，商加1。

再考虑不同符号的数的除法，比如 -8/3, 在这里要清楚其实不恢复余数的除法本质上还是恢复了余数，只不过和下一步的试商合在一起了。注意到上商的时候的判断标准和恢复余数的除法是不同的，不恢复余数的除法看的是是否和除数同号，这导致了本来该上 1 的地方现在上了 0，本来该上 0 的地方现在上了 1，相当于取反的效果，因此最后需要修正商，加一，合起来达到了取补码的效果。对于这种情况下余数修正的判断，如果最后余数符号和被除数相同，那么不需要修正，如果变了号，说明最后加过头了，但是没有下一轮来恢复了，这时需要减去一个除数。

但是在不同符号数相除的情形当中仍然有一个 bug，那就是正数除以负数且能整除的情况。比如 -8/2 ，我们会得到结果商为 -3,余数为 -2。试了一下，当被除数为负数，除数为正数，且可以整除的时候会出现这种情况。这时需要加一个特判修正，如果余数加上除数为0，那么商减一余数置0 。

2. 一些单位

我们目前所用的K、M、G、T等都是英文表示方法，分别是Kilo（10^3 )、Mega（10^6 ）、Giga（10^9 ）、Tera（10^12 ）的简写，更大的还有Peta（10^15 ）、Exa（10^18 ）、Bronto（10^21 ）等。

3. 机考注意点

3.1 整数除法固有bug

如果余数等于除数，那么余数减去除数，商加1。如果余数加上除数为0，那么商减一余数置0 。

3.2 原码整数乘法

注意进位参与结果右移。

3.2 浮点数相除

尾数相除时，用被除数加上除数的补码来判断是否够减，如果结果最高位是1就不够减，是0就够减。

SE-1 Review

发表于 2022-09-06 更新于 2023-02-18 分类于软件工程

Python部分

parameter是形参，argument是实参。
title() 方法返回一个字符串，其中每个单词的第一个字符均为大写。如果单词包含数字或符号，则其后的第一个字母将转换为大写字母。

换零钱问题（递归、动态规划）：给定半美元、25美分、10美分、5美分、1美分 5种硬币，将 1 美元换成硬币，有多少种硬币组合？
给定任意数量的现金和任意组合的硬币种类，计算换零钱所有方式的种数。

10 美分能够用到的硬币种类只有[10, 5, 1]三种。我们用 10$[10, 5, 1]这种记法来标记问题。先按币值为10的硬币来分类，将问题化为：

第一组，不使用 10 美分的硬币来表示，只用5美分和1美分来表示即 10$[5, 1]
第二组，使用了 10 美分的硬币，剩下的金额 0 使用全部的硬币种类表示，即 0$[10, 5, 1]

10$[10, 5, 1] = 10$[5, 1] + 0$[10, 5, 1] = 10$[1] + 5$[5, 1] + 0$[10, 5, 1] = 10$[1] + 5$[1] + 0$[5, 1] + 0$[10, 5, 1]

分成两组后，这两个问题新问题相对于原问题的范围缩小了，第一组现金没有变，但可选的硬币种类少了一种；第二组硬币种类没有变，但是现金减少了第一种硬币的币值。

边界问题如下：

当现金数 a 为 0 时，应该算作是有 1 种换零钱的方法
当现金数 a 小于 0 时，应该算作是有 0 种换零钱的方法
当换零钱可选的硬币种类为 0 时，应该算作是有 0 种换零钱的方法

按边界规则，可以直观看出，当金额为 0 或可选币种只有 1 种时，组合数都为 1。

一定要小心边界出口，仔细考虑设计边界条件

# -- coding = utf-8 --
def count_change(amount, coins_list):
    if amount == 0:
        return 1
    elif amount < 0 or not coins_list: 
        return 0
    else:
        part1 = count_change(amount, coins_list[1:])
        part2 = count_change(amount-coins_list[0], coins_list[:])
    return part1 + part2

us_coins = [1, 5, 10, 25, 50]
print(count_change(100, us_coins)

没有硬币种类换就返回0，amount<0防止

50$[20,10,5,1]->30$[20,10,5,1] - >10$[20,10,5,1]->10$[20,10,5,1]

思考递归问题时，先将其分解为几个子问题，然后分别判断这几个子问题在哪些方面缩减了问题的规模，以此来考虑边界情况。
在 Python 中，有一个特殊的常量 None（N 必须大写）。和 False 不同，它不表示 0，也不表示空字符串，而表示没有值，也就是空值。这里的空值并不代表空对象，即 None 和 []、“” 不同。

阅读全文 »